Robótica: Forward Kinematics en Python
marzo 31, 2010 1 comentario
Hace unas semanas encontré un curso online de la Universidad de Stanford de Introducción a la Robótica. El profesor es el reconocido Oussama Khatib y el curso es de licencia Creative Commons. Su principal contenido son 16 clases magistrales, pero también ofrecen un conjunto de ejercicios resueltos muy útiles. Me han servido para repasar algunos conceptos que aprendí en los cursos de doctorado. Hasta ahora he podido disfrutar las 5 primeras lecciones que se centran en la cinemática(kinematics) de un robot y me han parecido excelentes.
Por otra parte el último año, navegando en la web no he parado de toparme una y otra vez con librerías y herramientas de python orientadas a ámbitos científicos: Scipy, y Sage. Dado que no había utilizado nunca estas herramientas, pensé que era un buen momento para usarlas y de camino poner en práctica algunos conceptos teóricos básicos como la cinemática directa (forward kinematics) haciendo uso de la convención Denavit-Hartenberg. En cualquier caso recomiendo la cuarta y quinta clase magistral del curso de Stanford para el que quiera comprender claramente estos temas y sobre todo para el que quiera entender de donde salen las matrices que se usan en este post.
¿Qué es esto de la cinemática directa?
Pues es la técnica que permite obtener la configuración(posición y orientación) del end-effector (por ejemplo unas pinzas) de un robot articulado compuesto de links(enlaces) y joints(uniones). Hablando claro, una función que te dice donde está la punta del robot articulado según el estado del resto de articulaciones.
¿Que es esto del Denavit Hartenberg?
Se trata un método sistemático para describir los enlaces y uniones de un robot articulado e indica donde debemos colocar los frames para cada articulación de modo que pueda realizarse de forma sencilla la cinemática directa.
Objetivo
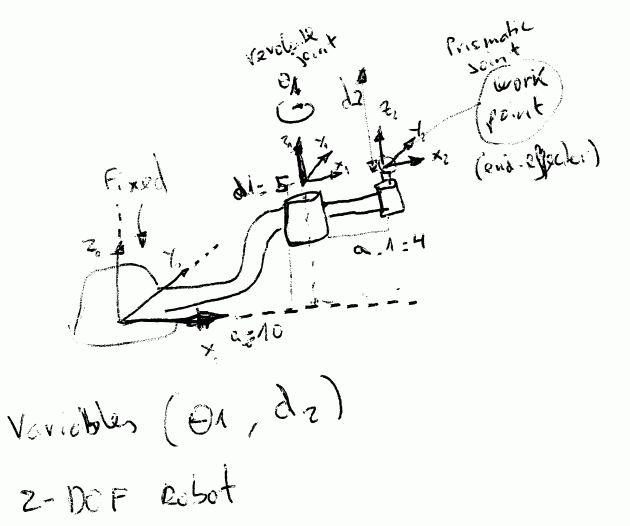
En resumen, mi objetivo es poner en práctica algunos de estos conceptos con herramientas de python como scipy.sympy y modelar matemáticamente un robot sencillo inventado(figura1, no le busquéis sentido al diseño :-D) con 2-DOF (theta_1,d_2).
1- Diseño del robot articulado
Se puede observar que el ejemplo propuesto es bastante sencillo: el robot tiene dos grados de libertad, con un revolute joint como primer joint y un prismatic joint como segundo joint. A continuación definimos formalmente los parámetros DH
| joint | a_(i-1) | alpha_(i-1) | d_i | theta_i |
|---|---|---|---|---|
| 1 | 10 | 0 | 5 | theta_1 |
| 2 | 4 | 0 | d_2 | 0 |
Se trata de un modelo sencillo ya que todos los ejes son perpendiculares al plano XY, por lo que no hay que hacer uso del parámetro alpha en ningún momento, y además permite libertad en la ubicación de los frames de ambos ejes. Por otra parte un par de comentarios de diseño:
- No se ha colocado el frame de la base fija junto con el primer joint (que es lo habitual y permite a_0=0 y alpha_0=0), el motivo es simplemente divulgativo para mostrar la diferencia entre ambos.
- Los frames de los dos ejes no están alineados con el frame fijo (lo que hubiera permitido d_1=0), sin embargo de esta manera el frame 2, indica la pose del end-effector y en otro caso habría que haber añadido otro frame con una transformación constante.
2- Cálculo de la matriz de transformación genérica en python
Bueno, la idea es sencilla, básicamente construir la matriz genérica de Forward Kinematics haciendo uso de la librería sympy que permite una notación simbólica (similar a Maple o Mathematica).
from sympy import *
theta_i=Symbol("theta_i")
alpha_i1=Symbol("alpha_i1")
a_i1=Symbol("a_i1")
d_i=Symbol("d_i")
T=Matrix([[cos(theta_i), -sin(theta_i), 0, a_i1],[sin(theta_i)*cos(alpha_i1),cos(theta_i)*cos(alpha_i1), -sin(alpha_i1), -sin(alpha_i1)*d_i],[sin(theta_i)*sin(alpha_i1), cos(theta_i)*sin(alpha_i1), cos(alpha_i1), cos(alpha_i1)*d_i],[0,0,0,1]])
print latex(T)
Vale, ya tenemos la matriz genérica, hagamos un ejemplo básico para comprobar si está bien. Por ejemplo, supongamos un robot, donde la siguiente articulación está en la misma posición del origen, su eje de giro es el eje Z, su desplazamiento en este eje 0 y que no ha girado nada. Teóricamente la configuración del end-effector tiene que ser el marco original, a ver una pequeña prueba:
T.subs(alpha_i1,0).subs(theta_i,0).subs(d_i,0).subs(a_i1,0) print latex(_)
Ok, obtenemos lo esperado, de momento continuamos. En el ejemplo de uso comprobaremos finalmente si ha habido algún error en el proceso 🙂
3- Matrices de transformaciones locales de cada joint
Haciendo uso de la matriz genérica obtenemos la matriz del primer joint (revolute joint) según los parametros DH:
theta_1=Symbol("theta_1")
T1=T.subs(alpha_i1,0).subs(a_i1,10).subs(d_i,5).subs(theta_i,theta_1)
print latex(T1)
Lo mismo para el segundo joint(prismatic joint).
d_2=Symbol("d_2")
T2=T.subs(alpha_i1,0).subs(a_i1,4).subs(theta_i,0).subs(d_i,d_2)
print latex(T2)
4 – Matriz de cinemática directa final
Pues ahora, simplemente, la matriz total que permite saber la posición del end-effector dados los parámetros variables theta_1 y d_2 es el producto de las anteriores:
Tt=T1*T2 print latex(Tt)
Bueno, entonces aquí tenemos la configuración del end-effector. Para el que no entienda como se interpreta esta matriz: básicamente se trata una matriz en coordenadas homogéneas, donde la última columna representa la posición y la sub-matriz 3×3 arriba a la izquierda (matriz de rotación) representa la posición de los tres ejes cartesianos del end-effector.
Se trata por supuesto de una descripción redundante ya que se podría haber hecho con solo 6 parámetros (3 posición + 3 rotación) en lugar de 16, sin embargo esta notación es la mas adecuada para el cálculo de la cinemática directa.
Por último para convertir esta expresión (matriz simbólica) en una función respecto a los dos parámetros variables utilizamos la función de sympy lamdify:
f=lambdify((theta_1,d_2),Tt,"numpy");
Ya está. Aquí tenemos la función de cinemática directa que acepta dos parámetros theta_1 y d_2 y nos devuelve la orientación y posición del end-effector.
5 – Ejemplo de uso
endEffectorConfiguration=Matrix(f(1.58,3)) print latex(endEffectorConfiguration)
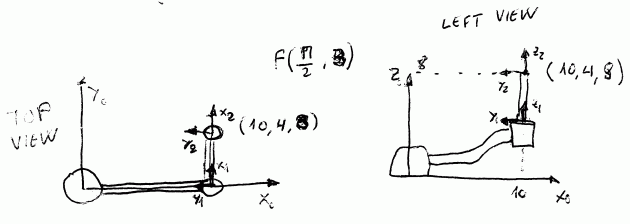
¡Y ya está! aquí está la matriz que describe el end-effector. Abajo os muestro una imagen sobre el estado del robot:
Probablemente muchos pensaréis que una matriz no es la forma mas clara de describir una pose en el espacio. Es cierto. Lo natural para nosotros es pensar en 6 parámetros (vector posición + tres ángulos). Existen varias alternativas para la representación con 6 parámetros, las mas conocidas son: fixed angles(absolute) o euler angles(relative). Estos parámetros están implícitamente en la mtriz y pueden extraerse. Sin embargo estas representaciones presentan problemas a la hora de tratar el movimiento continuo en el tiempo siguiendo trayectorias (¿a alguien le suena el efecto gimbal lock?). La solución es una representación de 7 parámetros llamada euler parameters(quaternions).
Comentarios finales
Python ofrece mecanismos para el cálculo sencillo de la cinemática directa de un robot No obstante existen frameworks de robótica con herramientas orientadas al cálculo de la cinemática directa por lo que no suele ser habitual tener que trabajar de la forma que se ha realizado en este post. Aquí os dejo algunas referencias de estos frameworks y librerías que yo he utilizado y me gustan por su calidad y/o flexibilidad:
- ROS y sus módulos kinematics y TF (transform)
- OROCOS y su módulo KDL (Kinematics and Dynamics)
- OpenRave
También se pueden encontrar ejemplos muy didácticos en la web comunitaria de matlab. Por último, veo en (robotic matlab toolkit) algunas referencias mas que pueden ser interesantes:
- •SPACELIB: 3D kinematics and dynamics, C-language and MATLAB. (Legnani, U. di Brescia)
- •Robotica for Mathematica (Spong, U. Ilinois), available but no longer supported.
- •C++ classes for robot kinematics and dynamics
- •Dynamechs a C++ library for simulating the dynamics of multibody systems
- •JRoboOp Java wrapper for ROBOOP from the PRISMA Lab at U. Naples.
- •MATROBCOM a toolbox for interfacing Matlab to real robots (Pires, U.Coimbra)
- •Open Dynamics Engine A free, industrial quality library for simulating articulated rigid body dynamics for example ground vehicles, legged creatures, and moving objects in VR environments.
- •Robot Symbolic Dynamics package for MAPLE (Corke, CSIRO)
- •ROBOMOSP: Robotics Modelling and Simulation Platform
- •ROBOOP developed by Richard Gourdeau of École Polytechnique de Montreal.
- •Robotics Toolbox for SciLab, Matteo Morelli
Have fun!



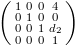


Pingback: Robótica: Inverse Kinematics (IK) en C++ con Orocos « GeuS' Blog: Robotics, Computer Science and More